Game Probabilities

Beneath the simple UI of our games lies a complex system. In this section, we’ll outline how probabilities and edges work across the YOLO Games suite.

Flipper

Flipper is just like an analog coin flip: there are two possible outcomes — either the coin lands on the player’s chosen side, or it doesn’t. The possibility of either of these outcomes is 50%.

If the player wins, they double their funds (minus a 2% fee on the payout, paid towards the liquidity pool and future incentives).

If the player loses, there’s no fee — but they also lose their funds.

With the probabilities involved, we can expect a player to win 50% of the time, thereby paying a 2% fee per game played.

Therefore, the edge in Flipper is 2%. Remember 1% of this goes back to the players via Future Incentives and 1% goes to the LP.

Quantum

In Quantum, players ‘hit’ Under or Over a given number that ranges between 0.1 and 95 (down to two decimal places). The multiplier associated with their selection can be calculated as follows:

$$m=\frac{100}{p}$$

Where m is the multiplier and p is the win probability.

TL;DR: the lower your chances of winning, the higher your multiplier.

As in Flipper, a 2% fee is taken from the total payout to the user.

Don’t Fall In

In Don’t Fall In, players are faced with a 5x5 grid of tiles. Their goal is to reveal them, avoiding lava pools along the way. We can calculate the probability of a given outcome occurring with the following equation:

$$p=\prod_{i=25}^{26-x}\frac{i-m}{i}$$

Where:

• p is the win probability
• x is the number of panels to reveal
• m is the number of lava pools

Like in Quantum, we use the following equation to compute multipliers for each given outcome:

$$m=\frac{100}{p}$$

Where m is the multiplier and p is the win probability.

Similarly, we take a 2% fee on the total payout to the user.

LaserBlast

In LaserBlast, players shoot a laser through rows of asteroids. It’ll eventually hit an alien with a multiplier attached to it, which dictates how much the player makes back.

The movement of the laser through the rows of asteroids follows a binomial distribution (e.g., where left indicates success, while right indicates failure). We use this to determine the probability that the player hits a specific alien. The probability of achieving r successes and n-r failures over n successive independent trials can be calculated as follows:

$$p=(1-P)^{n-r}P^{r}\frac{n!}{r!(n-r)!}$$

Where:

• p is the player’s probability of achieving r successes over n independent trials
• P is the success probability
• n is the number of successive independent trials
• r is the number of successes

The probability of the laser deviating to the left or the right of a mirror are identical — so (1-P) = P. This means we can simplify the equation by swapping out (1-P) with P, and using the Law of Exponents to add them together, since their base is identical:

$$p=P^{n}\frac{n!}{r!(n-r)!}$$

Let’s suppose that deviating to the right of a peg is a success. Given n rows of asteroids, this can happen between zero and n times. We’ll substitute P with 0.5 and n with the number of rows to calculate the probabilities for r successes taking place:

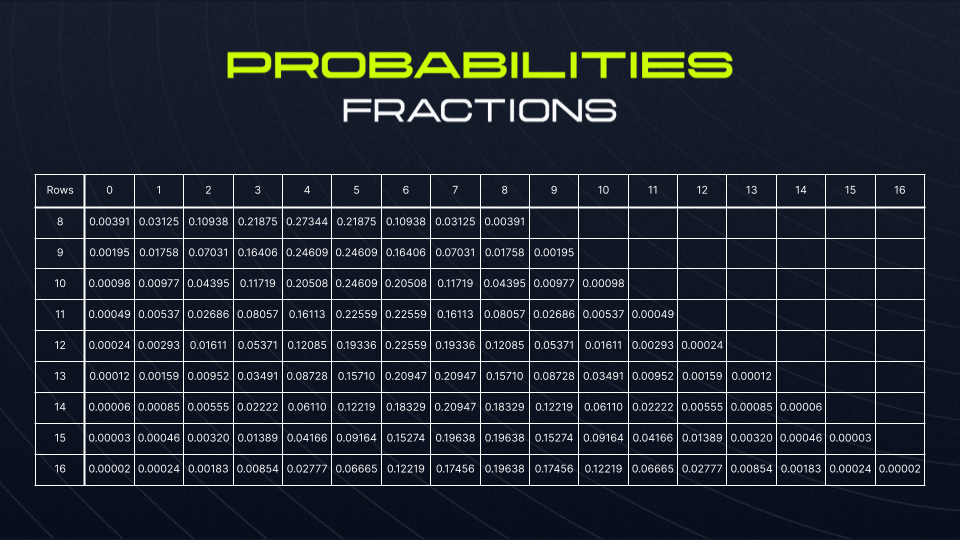
Note that, for any given row, all probabilities in a given row add up to 1.

The expected return for a row can be calculated as the sum of all probabilities of hitting each given alien by their respective multipliers. So let’s set the multipliers qualitatively such that the expected return is equal to 1.

In LaserBlast, there are three sets of multipliers to suit different risk tolerances. The higher-risk option results in an increase to the game’s variance. With this increase, a higher LP fee is taken to account for the higher temporary potential drawdown that liquidity pools may experience. The LP’s fee ranges from 1-2%, and is applied after a player has won alongside a 1% fee for Future Incentives.

The set multipliers can be seen below:

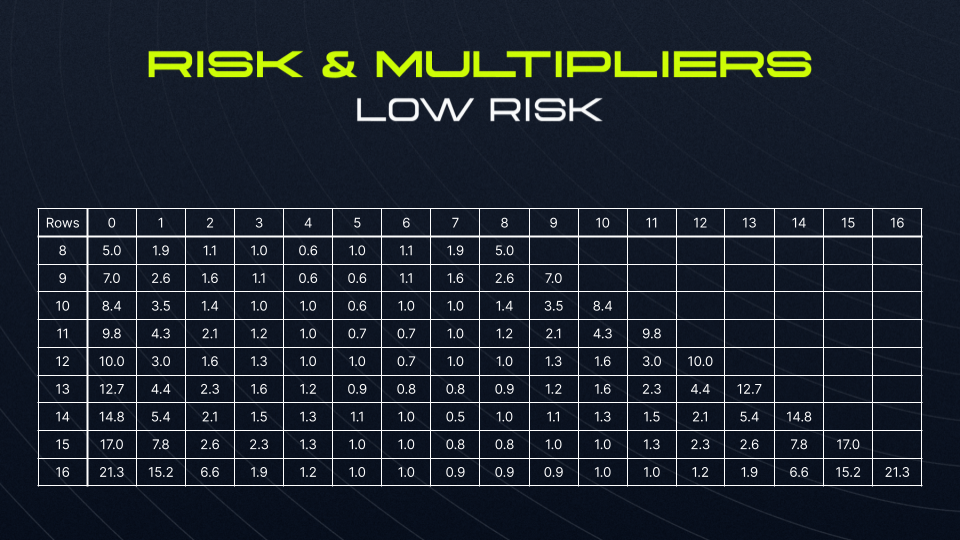
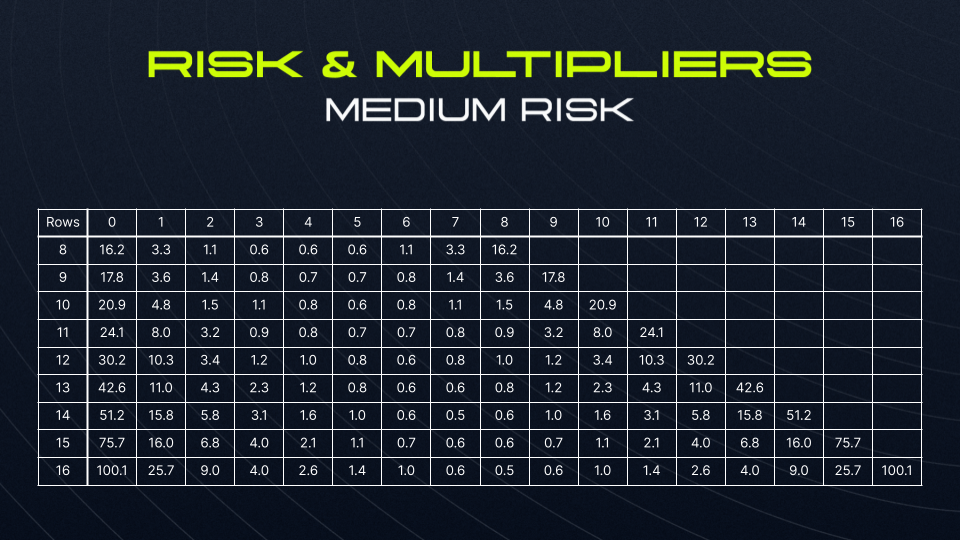
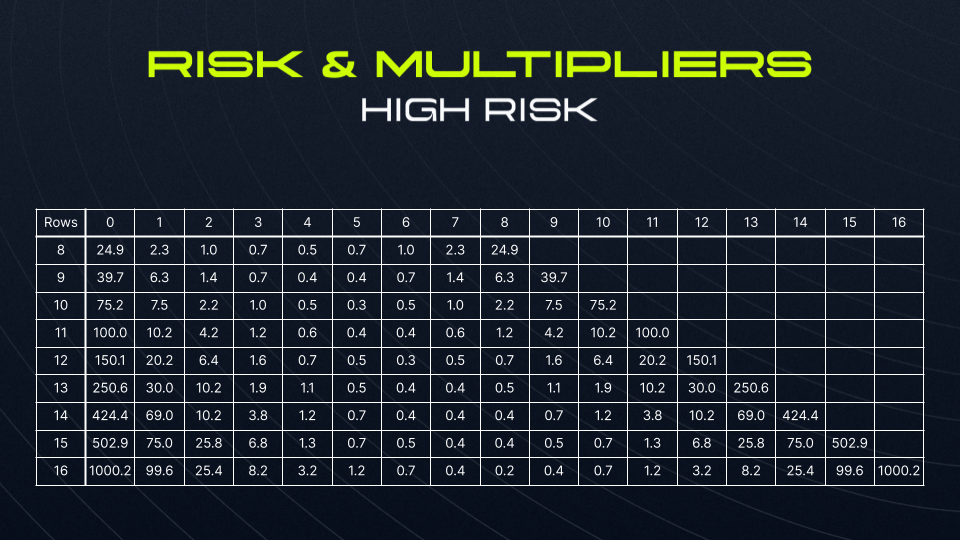
Now, let’s observe the expected returns, which are products of the multipliers and probabilities, and check that they sum to 1.

With multipliers and probabilities set, the player’s expected return (for a given number of rows and risk tolerance) can be calculated by taking the total of the probabilities for each outcome, multiplied by each of their respective multipliers.

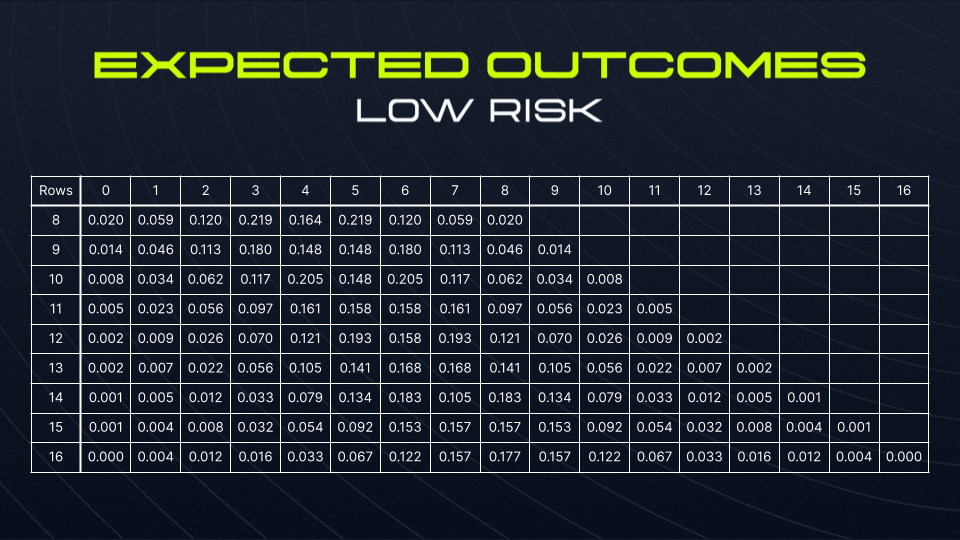
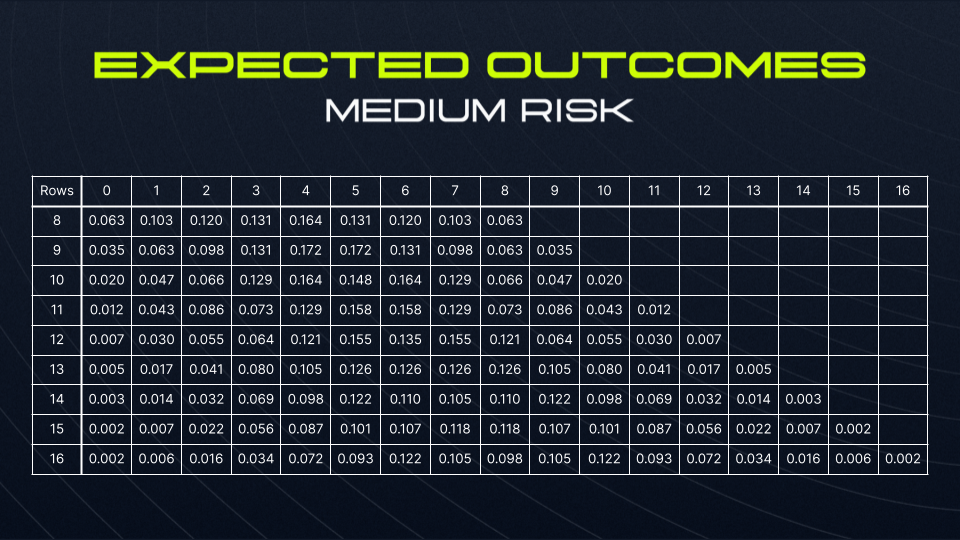
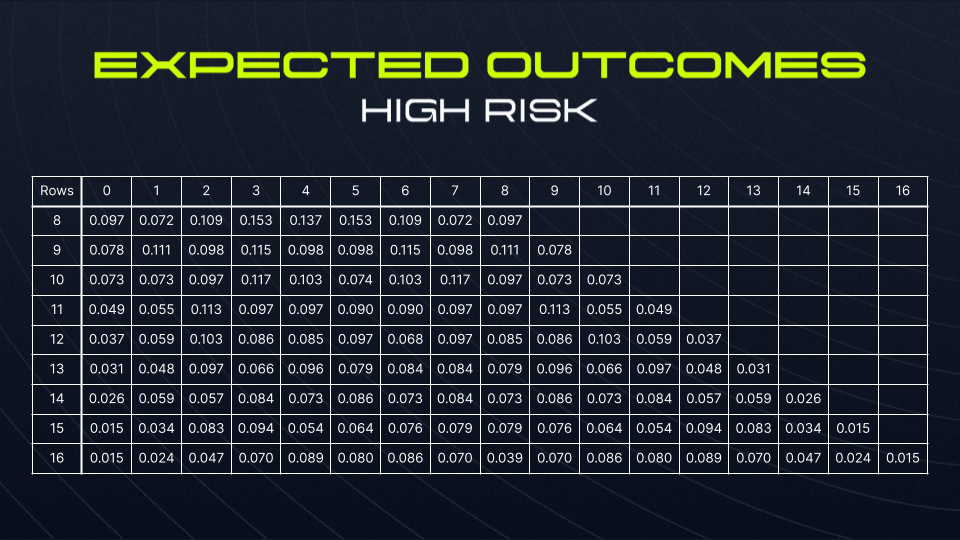
In all cases, the player has an expected return of 1 before any fees are applied. Therefore, the fee for the LP is simply the fee taken that the LP receives on a player’s win.